The rate equation for the breakdown of ES may be given by the sum of two reaction – one is the backward reaction of equation 1 and the other is the forward reaction of equation 2. Thus,

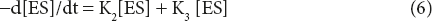
Assume the rate of formation of ES from E + P is very small (K₄), hence can be ignored.

When the reaction system enters the ‘steady state’ (defined as the condition in which the concentration of ES remains constant), the rate of formation of [ES] is equal to the rate of breakdown of [ES].

(5) = (6)

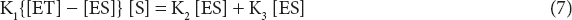
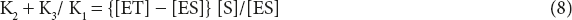
K₂ + K₃/K₁ = K_m where K_m is called Michaelis–Menten constant.

Thus,

Solving for [ES], we have

K_m [ES] = [ET] [S] − [ES] [S]
K_m [ES] + [ES] [S] = [ET] [S]
[ES] {K_m + [S]} = [ET] [S]

Substituting (10) in equation (3); V_o = K₃ [ES]

Now, if E is completely saturated with the substrate, V will increase to the maximum velocity V_max, which according to law of mass action, will be given by,

Substituting (12) in (11), we get

 

V_o = V_max [S]/K_m + [S]

This is the Michalis–Menten equation for a single substrate E catalysed reaction (Or equation for rectangular hyperbola) refer Figure 6.8. This equation adequately describes the kinetics of the most enzyme catalysed reactions (although the assumptions of these theories are not always correct, some exceptions exist).

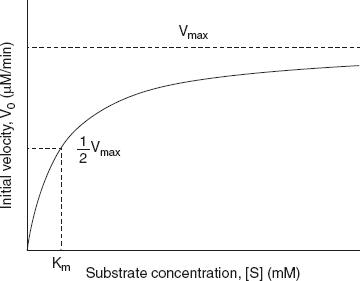
Figure 6.8 Michaklis Menten Plot (Hyperbola curve)